Table of Contents
Introduction
A hip roof has less attic volume than a gable roof, and in this article I explain why it’s less and how much less it is. Homeowners and builders should care about the difference in attic volume between hip and gable roofs because it directly affects usable attic space, insulation needs, ventilation requirements, and heating and cooling efficiency.
Note: For the sake of simplicity, the hip roofs and gable roofs discussed here are simple, regular hip roofs and gable roofs.
A regular gable roof is a simple, symmetrical roof with the following features:
- It has two sloped planes, one on each side of a central ridge.
- The ridge runs the full length of the building.
- The two sloped sides have the same pitch and meet at the top to form the ridge.
- The other two sides of the roof (the gable ends) are vertical triangular walls that rise from the eaves to the ridge as a continuation of the exterior walls of the building.
- The roof extends from eave to eave across the width of the building.
- The shape of the roof resembles an inverted “V” when viewed from the gable end.
This is the most common roof type on single-family homes and we are using it as the baseline for comparison when evaluating hip roofs.
A regular hip roof is a symmetrical roof where:
- All sides slope downward from a central ridge to the eaves.
- The ridge is centered along the long axis of a rectangular building.
- The roof has four sloped planes:
- Two longer sides (typically trapezoidal),
- Two shorter sides (hip ends, typically triangular or nearly so).
- The slopes on all four sides have the same pitch (slope angle).
- The ridge length is equal to the building length minus its width (R = L – W)
- The ridge is centered in the long dimension of the roof.
This type of hip roof is the most common in residential construction and is typically assumed in simplified formulas for calculating hip roof attic volume and surface area.
Why a Hip Roof Has Less Attic Volume Than a Gable Roof
A hip roof encloses less volume than a gable roof when both roofs have the same width, length, and vertical rise (height from eave to ridge), and therefore the same slope.
This is due to the shape of the roof ends:
- A gable roof has vertical triangle-shaped walls (gable ends) that allow the full triangular attic space to run the entire length of the building.
- A hip roof replaces those vertical walls with sloping roof planes, which taper inward and cut off the top corners of the gable attic. This eliminates the attic space that would exist in the triangular ends of a gable roof.
- So the difference comes from the hip ends, which slope in and up from the eave level at the ends of the roof and diagonally cut off the ends of the triangular prism that defines the attic space in a gable roof.
📐 Key Point:
Even though hip roofs and gable roofs have the same roof surface area for the same slope and footprint, hip roofs with the same slope and footprint do not have the same interior attic volume.
General Rule:
The difference in attic volume between a gable roof and a hip roof can be approximated by subtracting the volume of two triangular pyramids (also known as tetrahedrons) from the gable roof’s volume.
These pyramids represent the portions of space that are “cut off” at each end of the roof when you go from vertical gable walls to sloped hip ends.
Math:
If:
- W = building width (ft)
- L = building length (ft)
- H = vertical rise (ft)
- R = ridge length = L − W
Then:
Gable Roof Volume:
Vgable = (1⁄2) × W × H × L
Hip Roof Volume:
Vhip = Vgable − (1⁄6 × W × H × (L − R))
Since L − R = W, the subtracted volume becomes:
Subtracted Volume = (1⁄6) × W2 × H
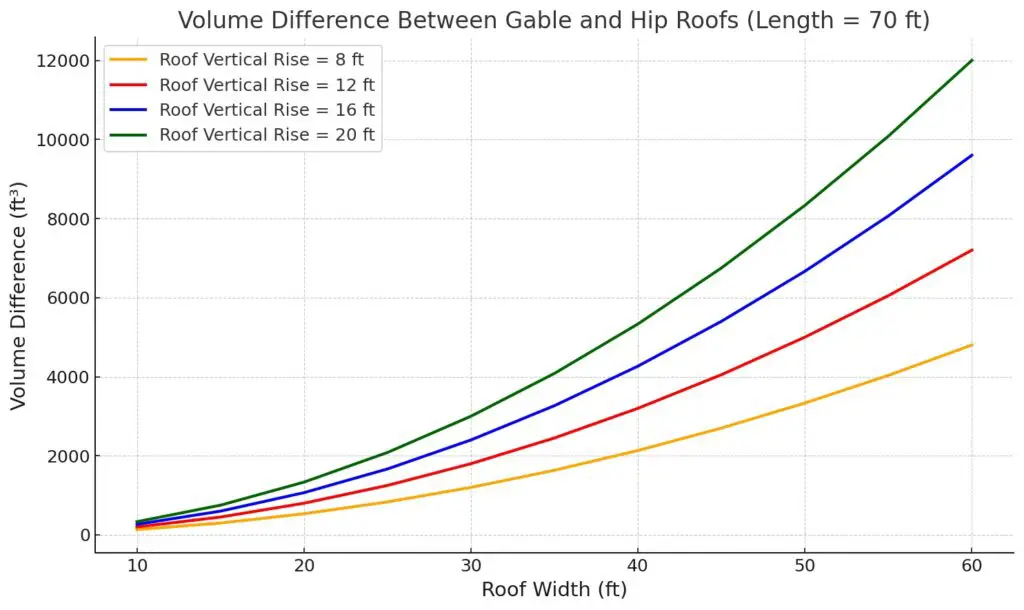
A hip roof encloses less attic volume than a gable roof with the same width, length, and vertical rise, due to the sloped hip ends that replace vertical gable walls.
The amount of volume less is always calculated as:
Subtracted Volume = (1⁄6) × Width² × Height
However, the percentage of volume less depends on the building’s proportions:
- For long, narrow buildings, the difference is smaller (around 10–15%)
- For wider or more square buildings, the difference can exceed 25%
Example 1: Typical House Shape
- Width: 40 ft
- Length: 70 ft
- Roof Height: 12 ft
Gable Roof Volume:
(½) × 40 × 12 × 70 = 16,800 ft³
Subtract Volume (hip ends):
(1⁄6) × 40² × 12 = 3,200 ft³
Hip Roof Volume:
16,800 − 3,200 = 13,600 ft³
% Less Volume:
(3,200 ÷ 16,800) × 100 ≈ 19%
Example 2: Long, Narrow Building
- Width: 30 ft
- Length: 100 ft
- Roof Height: 12 ft
Gable Roof Volume:
(½) × 30 × 12 × 100 = 18,000 ft³
Subtract Volume:
(1⁄6) × 30² × 12 = 1,800 ft³
Hip Roof Volume:
18,000 − 1,800 = 16,200 ft³
% Less Volume:
(1,800 ÷ 18,000) × 100 = 10%
Example 3: Nearly Square Building
- Width: 60 ft
- Length: 65 ft
- Roof Height: 12 ft
Gable Roof Volume:
(½) × 60 × 12 × 65 = 23,400 ft³
Subtract Volume:
(1⁄6) × 60² × 12 = 7,200 ft³
Hip Roof Volume:
23,400 − 7,200 = 16,200 ft³
% Less Volume:
(7,200 ÷ 23,400) × 100 ≈ 31%
Takeaway
While a hip roof attic always has a smaller volume than a gable roof attic, the volume difference between a hip roof attic and a gable roof attic grows larger as the building gets wider and more square (and as the roof grows steeper).
The percentage of space lost depends on the building’s proportions. Wider, squatter buildings lose a larger share of their attic volume under a hip roof than long, narrow ones.
About the Author
Jack Gray spent 20 years as a principal roof consultant with the Moriarty Corporation, an award-winning building enclosure consultant firm founded in 1967. Mr. Gray has worked in the roofing industry for over 25 years, with training and practical experience in roof installation, roof inspection, roof safety, roof condition assessment, construction estimating, roof design & specification, quality assurance, roof maintenance & repair, and roof asset management. He was awarded the Registered Roof Observer (RRO) professional credential in 2009. He also served as an infantry paratrooper in the 82nd Airborne Division and has a B.A. from Cornell University.