Category: Construction Calculators, Construction Math

Dome Roof Area Calculators (Spherical, Ellipsoid, Onion)

by
Jack Gray is an independent commercial roof consultant with over 25 years of experience in the roofing industry. He's trying to make the roofing information you find on the internet better, one article at a time.
A Studio Ghibli style version of the copper dome roof on 225 Liberty Street in Manhattan.
Yes, I Ghiblified the dome roof on 225 Liberty Street in Manhattan.

Introduction

There are several types of domes used as roofing features on buildings. Spherical domes are the most common. They have a uniform curvature and efficient load distribution. Ellipsoidal domes, which are shaped from a segment of an ellipsoid, are somewhat less common but frequently used in large-span structures where a lower height is desired. Elliptical domes, also referred to as oval domes, are a subtype distinguished by their elongated base; though architecturally striking, they are harder to build and relatively uncommon. Onion domes are probably the least used type of dome around these parts, but they are prominent in historical and cultural architecture in Russia, Eastern Europe, and Central Asia.

The surface area of most roofs can be calculated using basic length, width, and slope values. These calculations are very familiar to anyone involved in roofing, but domes don’t use these factors. I thought I’d put together a few calculators to help with calculating material requirements for dome roofs.

If you’re interested in domes more generally, you should check out the website of the Monolithic Dome Institute.

Spherical Domes

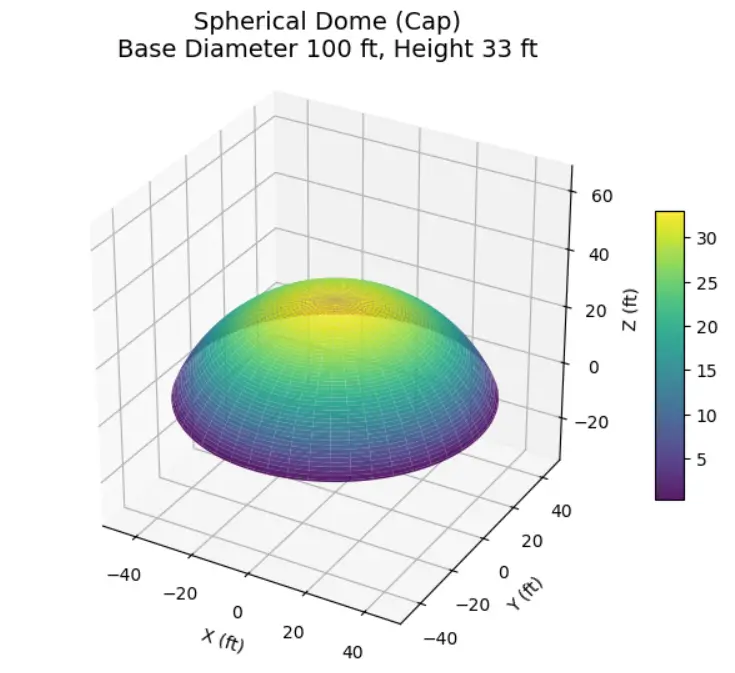
A computer graphic of a spherical dome roof produced using the output of the calculator.
Spherical dome generated using the logic of the calculator below. This is a spherical cap rather than a hemisphere.

A spherical dome is a portion of a sphere, typically resembling the upper half or less, used as a roof or structural covering. Geometrically, it’s defined as a segment of a sphere bounded by a circular base and the curved surface above it.

Characteristics of a Spherical Dome:

  • Shape: It follows the curvature of a sphere, meaning every point on its surface is equidistant from a central point located beneath the base.
  • Base: The bottom of the dome is a perfect circle, which is the boundary of the footprint of the dome.
  • Height and Radius: A spherical dome is characterized by its base radius and height. These two parameters determine how much of the sphere is used in the dome.
  • Surface: The surface is continuously curved, and its stable geometry allows for efficient load distribution as compressive forces travel along the curve to the base.

In architecture, spherical domes are used both for their visual impact and for their ability to cover large open spaces without internal supports.

Spherical Dome Roof Calculator

Enter your value in either the Dome Base Diameter or Dome Height field, or both.
• If only one input is provided, we calculate a hemisphere.
• If both inputs are provided, we calculate a spherical cap.

The math used in the calculator is explained below. See Spherical Dome Math Explanation.

Spherical Dome
Surface Area Calculator

Results:

Dome Surface Area (ft²):
Dome Base Radius (ft):
Dome Base Circumference (ft):
Footprint Area (ft²):
Dome Volume (ft³):

Results:

Dome Surface Area (m²):
Dome Base Radius (m):
Dome Base Circumference (m):
Footprint Area (m²):
Dome Volume (m³):

Ellipsoidal Domes

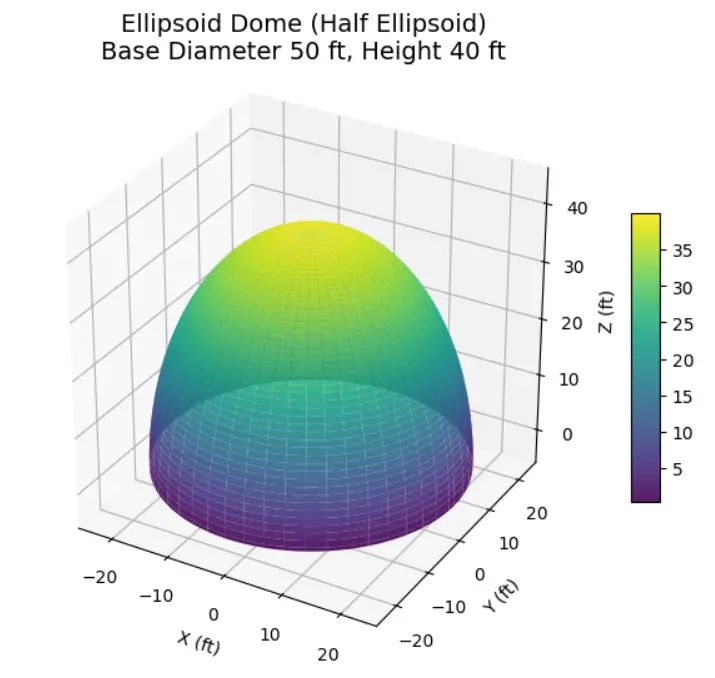
A computer graphic of an ellipsoidal dome roof produced using the output of the calculator.
A prolate ellipsoidal dome generated using the logic of the calculator below. Oblate domes are much more common, but they’re hard to tell apart from spherical domes.

An ellipsoidal dome roof is a curved roof structure that represents a segment of an ellipsoid, which is a three-dimensional shape formed by rotating an ellipse on one of its principal axes. Unlike a spherical dome, which has a uniform radius, an ellipsoidal dome has different radii along its horizontal and vertical axes. It looks like either a more elongated or more flattened version of a sphere.

Characteristics of an Ellipsoidal Dome Roof:

  • Shape: Derived from an ellipsoid, the dome may appear stretched vertically (prolate) or flattened (oblate), depending on the relative lengths of the major and minor axes of the ellipse.
  • Base: An ellipsoidal dome has a circular base. If a dome has an elliptical base, it’s called an elliptical dome.
  • Height-to-Span Ratio: Ellipsoidal domes typically have a lower height-to-span ratio than spherical domes, which can allow for a broader interior space under a lower profile.
  • Surface Curvature: The curvature changes more gradually compared to a spherical dome, providing a softer and more extended silhouette.

Ellipsoidal domes are often selected for their ability to span large areas while maintaining lower overall heights. Most ellipsoidal domes are oblate, meaning they are flatter than a spherical dome.

Ellipsoidal Dome Roof Calculator

Enter the dome dimensions in feet (USA) or meters (Metric). This calculator handles oblate (wider than tall) and prolate (taller than wide) ellipsoids. The calculator assumes your dome has a circular base.

The math used in the calculator is explained below. See Ellipsoidal Dome Math Explanation.

Ellipsoid Dome
Surface Area Calculator

Results:

Dome Surface Area (ft²):
Dome Base Radius (ft):
Dome Base Circumference (ft):
Footprint (ft²):
Dome Volume (ft³):

Onion Domes

An onion dome is a dome structure that features a distinctly bulging, rounded profile that curves outward from the base before narrowing sharply to a point or finial at the top. The shape resembles an onion or teardrop, often with a narrow base, swollen middle, and pointed crown.

Key Characteristics of an Onion Dome Roof:

  • Shape: Highly curved, with more dramatic vertical expansion than spherical or ellipsoidal domes.
  • Base: Typically circular, supporting the pronounced upward swell.
  • Function: The form helps prevent snow accumulation on the roof and can reduce wind loads.
  • Design Context: Often seen in Eastern Orthodox architecture.

Structurally complex, onion domes are striking architectural features that merge engineering with cultural expression. Onion domes, with their swelling midsections and tapering tops, are not just stylistic; their form can help reduce snow accumulation and wind pressure.

Onion Dome Roof Calculator

A computer graphic of an onion dome produced using the output of the calculator.
This is the shape of the model onion dome used by the calculator below.

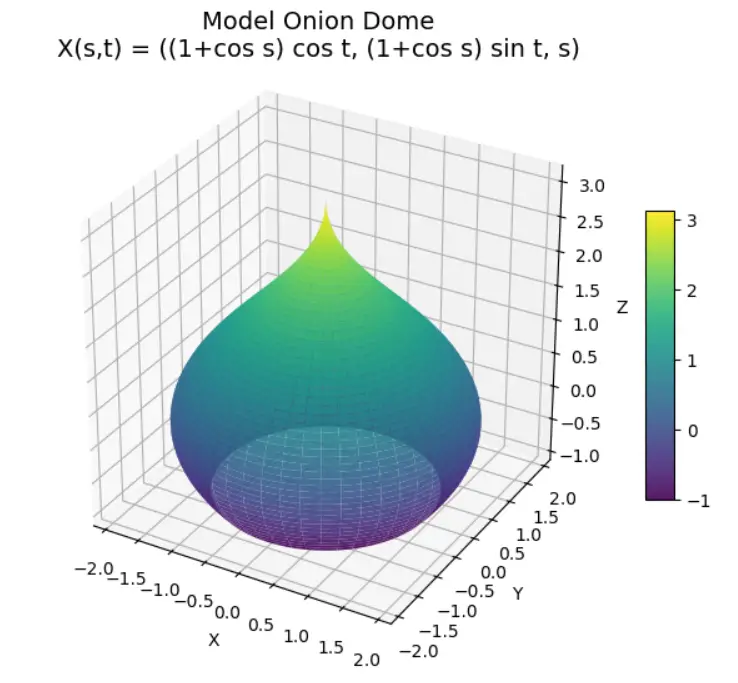
This calculator uses a parametric model for an onion dome. In the model, the dome is given by:
X(s, t) = ((1 + cos s) cos t, (1 + cos s) sin t, s), for s ∈ [–π/3, π] and t ∈ [0, 2π].

For a dome of height H, the model is uniformly scaled in either feet (USA) or meters (Metric).

The math used in this calculator is explained here.

This calculator will only calculate values for our model onion dome. The only variable you can enter is height; the calculator will adjust the calculations based on height and the fixed model parameters. You cannot adjust the width of the dome relative to the height. All domes calculated by this calculator have the same shape, even if they have different heights.

Onion Dome Surface Area Calculator

Results:

Dome Height (ft):
Base Diameter (ft):
Onion Dome Surface Area (ft²):

More about the onion dome calculator:

In this model, the dome is described by a function X(s, t) that returns a three-dimensional point. The equation is:

  X(s, t) = ((1 + cos(s))·cos(t), (1 + cos(s))·sin(t), s)

Here’s what each part means:

• The first coordinate, (1 + cos(s))·cos(t), and the second coordinate, (1 + cos(s))·sin(t), determine the horizontal position (the x and y coordinates). The term (1 + cos(s)) gives the radius at a particular height.

• The third coordinate, s, directly represents the vertical position (or height) of the dome.

• The parameter s varies from –π/3 to π. When s equals –π/3, the dome has its maximum base radius (since cos(–π/3) = 0.5, making the radius 1.5), and when s equals π, cos(π) is –1, so the radius becomes zero. This means the dome tapers smoothly to a point at the top.

• The parameter t runs from 0 to 2π, covering a full rotation around the vertical axis, which creates the dome’s circular symmetry.

This parameterization yields a surface that captures the distinctive rounded, tapering shape of an onion dome, as seen on many traditional Russian Orthodox churches.

How to Tell a Spherical Dome from an Ellipsoid Dome

When both domes have a circular base, the difference lies in the curvature of the dome itself:

  • Uniform Curvature vs. Varying Curvature:
    A spherical dome is a spherical cap. A spherical cap is defined as a section of a sphere cut off by a plane; its curvature is uniform in every direction. In every vertical or horizontal slice through the center, the dome will show the same circular arc. On the other hand, an ellipsoidal dome (even with a circular base) is a portion of an ellipsoid; the curvature in the vertical direction is different from that in the horizontal plane.
  • Relationship Between Dome Height and Base Radius:
    For a true hemisphere (which is a type of spherical dome), the dome height will equal the base radius. In an ellipsoidal dome with a circular base, the dome height generally differs from the base radius, typically being less (oblate ellipsoids) because the dome’s vertical profile is more “flattened” compared to a portion of a perfect sphere.
  • Cross‑Sectional Profiles:
    A vertical cross section through the dome will reveal its true shape. For a spherical dome, the arc of the dome will be part of a circle. For an ellipsoidal dome, the arc will be elliptical; the curve will not match a circular arc perfectly, and the measured curvature will vary from the horizontal (base) to the apex.

In practice, you can tell the difference by:

  • Measuring the dome height vs. the base radius: If they’re equal (or nearly equal), the dome is likely spherical; significant differences suggest an ellipsoidal shape.
  • Performing curvature measurements: Uniform curvature everywhere indicates a sphere; varying curvature indicates an ellipsoid.
  • Inspecting cross-sectional profiles: A perfect circular arc in a vertical cross-section means a spherical dome; an elliptical arc points to an ellipsoidal dome.

Spherical Dome Math Explanation

Here's an overview of how the Spherical Dome Calculator produces each of its 5 outputs (Surface Area, Base Radius, Base Circumference, Footprint Area, and Volume). The calculator has two modes depending on how many inputs you provide:

  • Hemisphere Mode (exactly one input: either diameter or height)
  • Spherical Cap Mode (two inputs: both diameter and height)

1) Hemisphere Mode (One Input)

If the user enters exactly one valid value (e.g., base diameter but not height, or vice versa), the code assumes a hemisphere.

Key Geometry

• Radius r is taken to be half the base diameter or (if only height is given) the height.
• If a diameter d is provided, then r = d/2, and the dome height is r as well (since a hemisphere’s height equals its radius).
• Conversely, if a height h is provided, then r = h and d = 2h.

Outputs (Hemisphere)

  • Dome Base Radius = r
  • Dome Base Circumference = 2πr
  • Footprint Area = π (r2)
  • Dome Surface Area (hemisphere) = 2π(r2)
  • Dome Volume (hemisphere) = (2/3) π (r3)

2) Spherical Cap Mode (Two Inputs)

If the user enters both a base diameter d and a height h, the dome is treated as a spherical cap rather than a hemisphere.

Key Geometry

• Base Radius a = d/2
• The code then computes the “radius of curvature” R of the original sphere: R = (a² + h²) / (2h)

Outputs (Spherical Cap)

  • Dome Base Radius = a
  • Dome Base Circumference = 2πa
  • Footprint Area = π(a2)
  • Dome Surface Area (cap) = π (a2 + h2)
  • Dome Volume (cap) = [ π(h2)(3R − h ) ] / 3, where R = (a2 + h2) / (2h).

Summary of Formulas

Hemisphere (one dimension): If r = d/2 or r = h, then: Surface Area = 2π(r2), Circumference = 2πr, Footprint = π(r2), Volume = (2/3)π(r3).

Spherical Cap (two dimensions, diameter d and height h): a = d/2. Surface Area = π(a2 + h2), Volume = [π(h2)(3R − h)] / 3, where R = (a2 + h2) / (2h).

Hence, the calculator automatically picks the hemisphere or spherical cap formulas based on how many inputs (diameter/height) you provide, and outputs these five results accordingly.

Ellipsoidal Dome Math Explanation

The Ellipsoidal Dome Calculator treats your dome as a vertical ellipsoidal cap. You enter a “base diameter” (d) and a “dome height” (h). Depending on whether ½d ≥ h (oblate) or ½d < h (prolate), slightly different formulas apply for surface area. (A dome with ½d = h is actually a spherical dome as radius r = h defines a hemisphere.)

Geometry

  • Base Radius: r = d/2. The calculator uses r and h as the ellipse’s semi-axes.
  • Base Circumference: 2πr
  • Footprint (area of the circular base): πr2

Surface Area

The dome’s curved area is half an oblate or prolate ellipsoid. We let r = horizontal radius, h = vertical height, and compute:

  • Oblate Case (if h ≤ r):
    e = √[1 – (h2 / r2)] atanh(e) = standard inverse hyperbolic tangent function.

    Surface Area (half oblate) =
    πr2 × [ 1 + ((1 – e2) / e) × atanh(e) ]
  • Prolate Case (if h > r):
    e = √[1 – (r2 / h2)] asin(e) = standard inverse sine function.

    Surface Area (half prolate) =
    ½ × [ 2πr2 + (2πr×h / e) × asin(e) ]

Volume

An entire ellipsoid volume is (4/3)π(r2)h (assuming r = “equatorial” radius, h = “polar” semi-axis). The dome is half of that:

Dome Volume = (2/3)π(r2) × h

Putting It All Together

For each mode (USA or Metric), the calculator interprets the units (feet or meters), sets r = (diameter / 2), h = dome height, then picks the oblate or prolate formula for surface area, and computes:

  1. Dome Roof Base Radius = r
  2. Dome Roof Base Circumference = 2πr
  3. Footprint = πr2
  4. Dome Roof Surface Area (using the oblate or prolate formulas above)
  5. Dome Roof Volume = (2/3) × π × r2 × h

This ensures correct results whether your dome is “wider than tall” (oblate) or “taller than wide” (prolate).