I participate in the Amazon affiliate program and may earn commissions from purchases made through links on this page.
Table of Contents
- Quick Reference: Common Roof Pitches in Degrees
- Introduction
- Calculator: Roof Pitch and Degrees Conversion
- How to Convert Standard Roof Pitch to Degrees
- Table 1: Standard Roof Pitch to Degrees
- How to Convert Roof Angle in Degrees to Standard Roof Pitch
- Table 2: Roof Angles in Degrees to Standard Roof Pitch
- Useful Roof Slope Tools
Quick Reference: Common Roof Pitches in Degrees
| Roof pitch | Degrees | In plain English |
|---|---|---|
| 1/12 | 4.76° | your 1 in 12 roof pitch has a 4.76 degree roof angle |
| 2/12 | 9.46° | your 2 in 12 roof pitch has a 9.46 degree roof angle |
| 3/12 | 14.04° | your 3 in 12 roof pitch has a 14.04 degree roof angle |
| 4/12 | 18.43° | your 4 in 12 roof pitch has an 18.43 degree roof angle |
| 5/12 | 22.62° | your 5 in 12 roof pitch has a 22.62 degree roof angle |
| 6/12 | 26.57° | your 6 in 12 roof pitch has a 26.57 degree roof angle |
| 7/12 | 30.26° | your 7 in 12 roof pitch has a 30.26 degree roof angle |
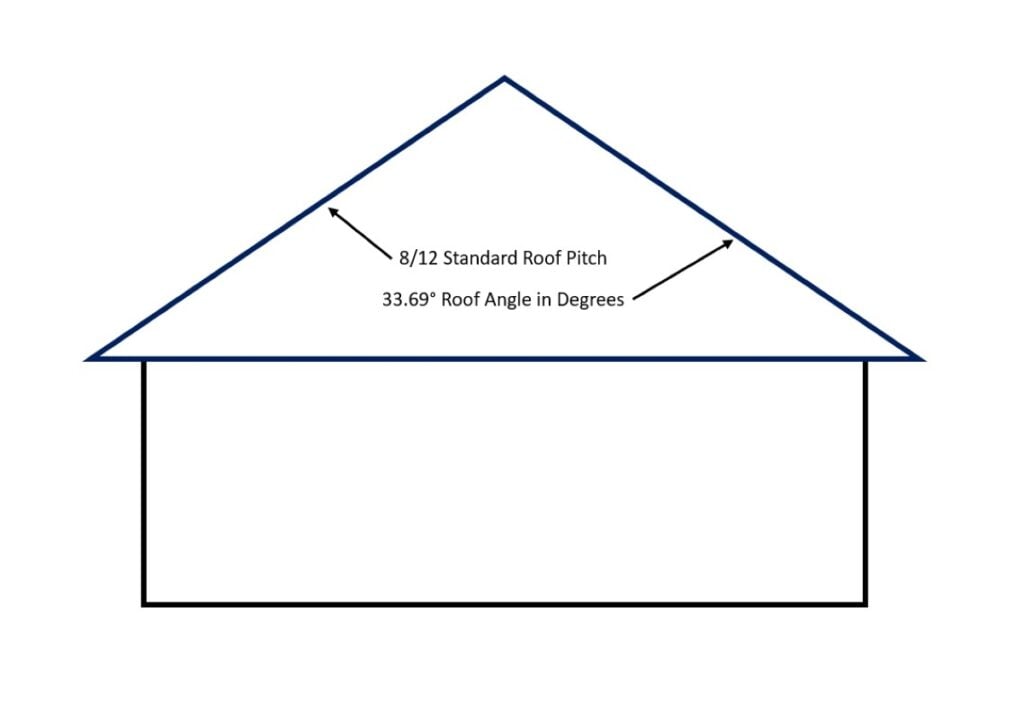
| 8/12 | 33.69° | your 8 in 12 roof pitch has a 33.69 degree roof angle |
| 9/12 | 36.87° | your 9 in 12 roof pitch has a 36.87 degree roof angle |
| 10/12 | 39.81° | your 10 in 12 roof pitch has a 39.81 degree roof angle |
| 11/12 | 42.51° | your 11 in 12 roof pitch has a 42.51 degree roof angle |
| 12/12 | 45.00° | your 12 in 12 roof pitch has a 45 degree roof angle |
Tip: If you need a pitch that is not listed here, use the calculator below for any custom value.
Introduction
There are a few reasons why you’d want to convert roof pitch to degrees or convert a roof slope in degrees to standard roof pitch. But the main issue that comes to mind is the fact that technical literature relating to specific roofing products or roof design often use one or the other, but not both.
This is definitely a problem for English-speaking people outside of the United States reading American roofing literature, and vice versa. Say you’re used to standard roof pitch, you’re checking out a new roofing product on a foreign company’s website, and you read that the product has a minimum slope requirement of 20°. It can slow you down. This page should make all that easier.
If you’re not sure what the slope of your roof is and you want to know that (in either degrees or rise-in-run), I recommend this slope finder on Amazon. It’s very inexpensive and very accurate. You may also want to consider getting yourself a construction calculator. This one is very good.
Note: Correct Format When Stating Roof Pitch
When discussing roof pitch, the proper way to state a specific pitch is in the form “X-in-12”, so if you’re talking about a roof that rises 6 units for every 12 units it runs horizontally, you would say that the roof has a 6 in 12 pitch. In roofing industry literature, the standard abbreviation used for indicating a particular roof pitch has a colon and takes the form “X:12” or “X : 12”, so for a 6 in 12 pitch, you would write “6:12 pitch”.
As a practical matter, an overwhelming number of people looking for information about roof pitch on the internet search for a roof pitch using a slash, as in “6/12”. In order to help more people find what they’re looking for, I am using the “X/12” form in several places here. I’m not a purist in this case.
Calculator: Roof Pitch and Degrees Conversion
This calculator converts roof pitch (X-in-12) to degrees and degrees to roof pitch, including decimal values, with results shown to two decimal places.
How to Convert Standard Roof Pitch to Degrees
Conversion Formula for Standard Roof Pitch to Degrees
This is how you convert a slope expressed in standard roof pitch (even a slope that include a fraction) to degrees:
- To convert a roof slope expressed as “X-in-12″ to a roof slope expressed in degrees, find the arctangent of (rise/run).
- Divide the rise (that’s the “X”, your “X” will vary according to how steep the roof is) by the run (the run is always 12).
- Using a scientific calculator, find the arctangent of the result.
There’s a good scientific calculator here at web2.0calc.com. Click the “2nd” button (top left of the calculator field). The “atan” (arctangent) button is the second from the bottom on the left side of the calculator field.
First enter the number you got from dividing your rise by your run (0.791667 in the following example).
Then click the “atan” button, and then the “=” button. This will give you the arctangent of (rise/run).
Example:
- For a slope of 9½-in-12
- Convert to a decimal: 9½ becomes 9.5
- Divide 9.5 by 12 (rise/run is 9.5/12) to get 0.791667
- Find the arctangent of 0.791667
- Arctan(0.791667) = 38.367497125297
- Round this to a reasonable number of digits. Let’s call it 38.37.
- A 9½-in-12 roof slope is the same as a 38.37 degree slope.
Table 1: Standard Roof Pitch to Degrees
The following table shows the degree equivalents for all roof slopes in standard pitch from ⅛-in-12 to 36½-in-12. To see the percentage equivalents for standard rise-in-run roof pitches, see Three Ways to Express Roof Slope. That article also explains the math that allows you to convert any roof slope expressed in any way to any other way (pitch to degrees, percentage to degrees, degrees to percentage, etc.).
| Standard Roof Pitch(Roof Slope as X in 12) | Roof Angle(In Degrees) |
|---|---|
| 0.125 in 12 (1/8 in 12) | 0.60° |
| 0.25 in 12 (1/4 in 12) | 1.19° |
| 0.5 in 12 (1/2 in 12) | 2.39° |
| 1/12 | 4.76° |
| 1.5/12 | 7.13° |
| 2/12 | 9.46° |
| 2.5/12 | 11.77° |
| 3/12 | 14.04° |
| 3.5/12 | 16.26° |
| 4/12 | 18.43° |
| 4.5/12 | 20.56° |
| 5/12 | 22.62° |
| 5.5/12 | 24.62° |
| 6/12 | 26.57° |
| 6.5/12 | 28.44° |
| 7/12 | 30.26° |
| 7.5/12 | 32.01° |
| 8/12 | 33.69° |
| 8.5/12 | 35.31° |
| 9/12 | 36.87° |
| 9.5/12 | 38.37° |
| 10/12 | 39.81° |
| 10.5/12 | 41.19° |
| 11/12 | 42.51° |
| 11.5/12 | 43.78° |
| Standard Roof Pitch(Roof Slope as X in 12) | Roof Angle(In Degrees) |
|---|---|
| 12/12 | 45° |
| 12.5/12 | 46.17° |
| 13/12 | 47.29° |
| 13.5/12 | 48.37° |
| 14/12 | 49.4° |
| 14.5/12 | 50.39° |
| 15/12 | 51.34° |
| 15.5/12 | 52.25° |
| 16/12 | 53.13° |
| 16.5/12 | 53.97° |
| 17/12 | 54.78° |
| 17.5/12 | 55.56° |
| 18/12 | 56.31° |
| 18.5/12 | 57.03° |
| 19/12 | 57.72° |
| 19.5/12 | 58.39° |
| 20/12 | 59.04° |
| 20.5/12 | 59.66° |
| 21/12 | 60.26° |
| 21.5/12 | 60.83° |
| 22/12 | 61.39° |
| 22.5/12 | 61.93° |
| 23/12 | 62.45° |
| 23.5/12 | 62.95° |
| 24/12 | 63.43° |
| Standard Roof Pitch(Roof Slope as X in 12) | Roof Angle(In Degrees) |
|---|---|
| 24.5/12 | 63.90° |
| 25/12 | 64.36° |
| 25.5/12 | 64.80° |
| 26/12 | 65.22° |
| 26.5/12 | 65.64° |
| 27/12 | 66.04° |
| 27.5/12 | 66.43° |
| 28/12 | 66.80° |
| 28.5/12 | 67.17° |
| 29/12 | 67.52° |
| 29.5/12 | 67.86° |
| 30/12 | 68.20° |
| 30.5/12 | 68.52° |
| 31/12 | 68.84° |
| 31.5/12 | 69.15° |
| 32/12 | 69.44° |
| 32.5/12 | 69.73° |
| 33/12 | 70.02° |
| 33.5/12 | 70.29° |
| 34/12 | 70.56° |
| 34.5/12 | 70.82° |
| 35/12 | 71.08° |
| 35.5/12 | 71.32° |
| 36/12 | 71.57° |
| 36.5/12 | 71.80° |
How to Convert Roof Angle in Degrees to Standard Roof Pitch
Conversion Formula for Degrees to Standard Roof Pitch
This is how you convert a slope expressed in degrees (even a slope that include a fraction of a degree) to standard roof pitch:
- Find the tangent of the degree value.
- Multiply the tangent by the run (in roofing, the run is always 12 by convention).
- That gives you the rise. Put them together as Rise-in-Run.
You can find a good calculator here at web2.0calc.com. Enter your degree value, click the “tan” button, then click the “=” button. Multiply that result by 12. That result is your standard roof pitch value.
Example:
For a slope of 35.5°:
- tan(35.5) = 0.713
- 0.713 x 12 = 8.556
- giving you a slope of 8.556-in-12 or approximately 8-9/16 in 12.
Table 2: Roof Angles in Degrees to Standard Roof Pitch
The following table shows the roof pitch (rise-in-run) equivalents for all roof slopes in degrees from 1° to 72°. Other than the 45° roof slope, which is 12-in-12, none of the standard roof pitches (5-in-12, 6-in-12, etc.) are equal to a whole degree.
| Roof Angle(In Degrees) | Standard Roof Pitch(Roof Slope as X in 12) |
|---|---|
| 1° | 0.209 in 12 |
| 2° | 0.419 in 12 |
| 3° | 0.629 in 12 |
| 4° | 0.839 in 12 |
| 5° | 1.050 in 12 |
| 6° | 1.261 in 12 |
| 7° | 1.473 in 12 |
| 8° | 1.686 in 12 |
| 9° | 1.901 in 12 |
| 10° | 2.116 in 12 |
| 11° | 2.333 in 12 |
| 12° | 2.551 in 12 |
| 13° | 2.770 in 12 |
| 14° | 2.992 in 12 |
| 15° | 3.215 in 12 |
| 16° | 3.441 in 12 |
| 17° | 3.669 in 12 |
| 18° | 3.899 in 12 |
| 19° | 4.132 in 12 |
| 20° | 4.368 in 12 |
| 21° | 4.606 in 12 |
| 22° | 4.848 in 12 |
| 23° | 5.094 in 12 |
| 24° | 5.343 in 12 |
| Roof Angle(In Degrees) | Standard Roof Pitch(Roof Slope as X in 12) |
|---|---|
| 25° | 5.596 in 12 |
| 26° | 5.853 in 12 |
| 27° | 6.114 in 12 |
| 28° | 6.381 in 12 |
| 29° | 6.652 in 12 |
| 30° | 6.928 in 12 |
| 31° | 7.210 in 12 |
| 32° | 7.498 in 12 |
| 33° | 7.793 in 12 |
| 34° | 8.094 in 12 |
| 35° | 8.402 in 12 |
| 36° | 8.719 in 12 |
| 37° | 9.043 in 12 |
| 38° | 9.375 in 12 |
| 39° | 9.717 in 12 |
| 40° | 10.069 in 12 |
| 41° | 10.431 in 12 |
| 42° | 10.805 in 12 |
| 43° | 11.190 in 12 |
| 44° | 11.588 in 12 |
| 45° | 12.000 in 12 |
| 46° | 12.426 in 12 |
| 47° | 12.868 in 12 |
| 48° | 13.327 in 12 |
| Roof Angle(In Degrees) | Standard Roof Pitch(Roof Slope as X in 12) |
|---|---|
| 49° | 13.804 in 12 |
| 50° | 14.301 in 12 |
| 51° | 14.819 in 12 |
| 52° | 15.359 in 12 |
| 53° | 15.925 in 12 |
| 54° | 16.517 in 12 |
| 55° | 17.138 in 12 |
| 56° | 17.791 in 12 |
| 57° | 18.478 in 12 |
| 58° | 19.204 in 12 |
| 59° | 19.971 in 12 |
| 60° | 20.785 in 12 |
| 61° | 21.649 in 12 |
| 62° | 22.569 in 12 |
| 63° | 23.551 in 12 |
| 64° | 24.604 in 12 |
| 65° | 25.734 in 12 |
| 66° | 26.952 in 12 |
| 67° | 28.270 in 12 |
| 68° | 29.701 in 12 |
| 69° | 31.261 in 12 |
| 70° | 32.970 in 12 |
| 71° | 34.851 in 12 |
| 72° | 36.932 in 12 |
Useful Roof Slope Tools
If you’re not sure what the slope of your roof is and you want to measure it, in either degrees or standard roof pitch, I recommend this slope finder on Amazon. It’s very inexpensive and very accurate. I have one and it works well.
If you want to know the slope of anything to an amazing degree of accuracy and you like cool new tools, you should check out this digital level. That level may be way too expensive for what you need, but this is what professionals use, so I thought I’d mention it. It will tell you the slope of your roof in degrees, rise/run, or percentage, and automatically convert from one to the other. In other words, it will do everything this article explains how to do.
Also, if you’re looking things up on this web page, you may want to get yourself a construction calculator. This one is very good.

